Report

Group: 2
Section: 9

Wojciech Bieniek
Patryk Piwowarczyk
Aleksandra Szpiech

Ex. 3

Tutor name: Damian Grzechca

C1 L2

$f_{IN} = 186Hz$
$T_{resp} = 1.04ms$
Measurement of oscillation period

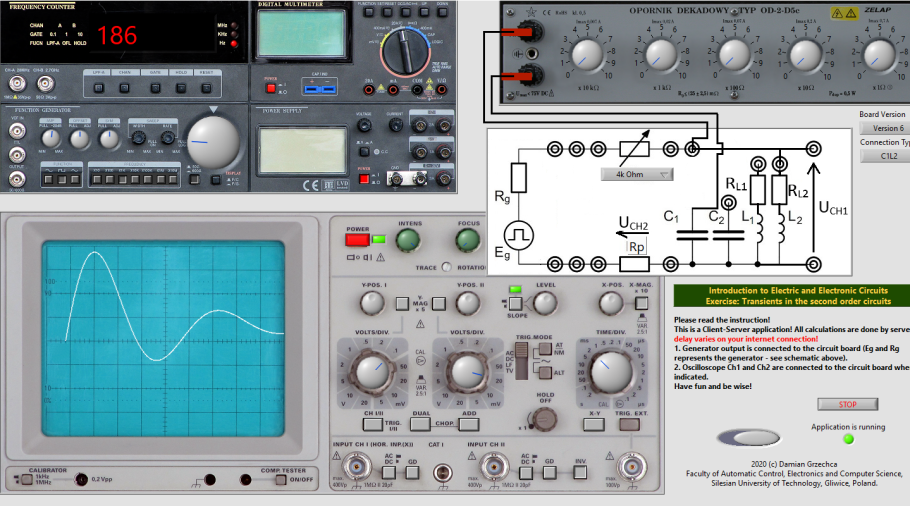
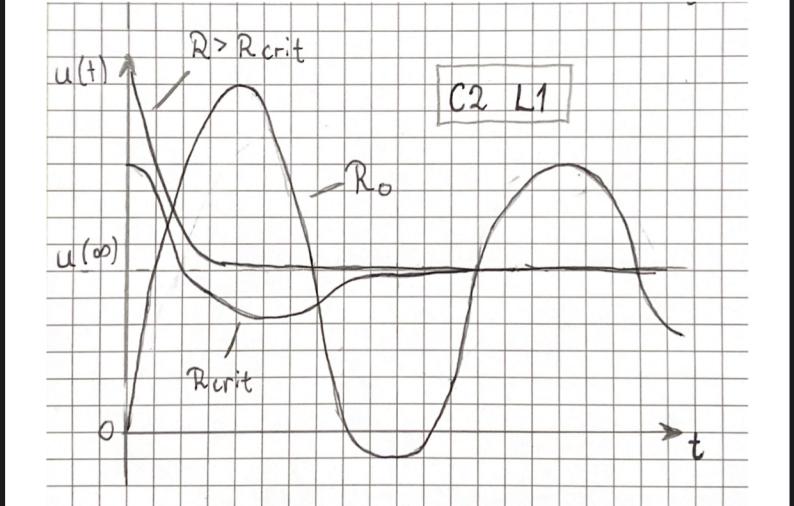
Critical response $R_{crit} = 150 \Omega$

Observed voltage characteristic

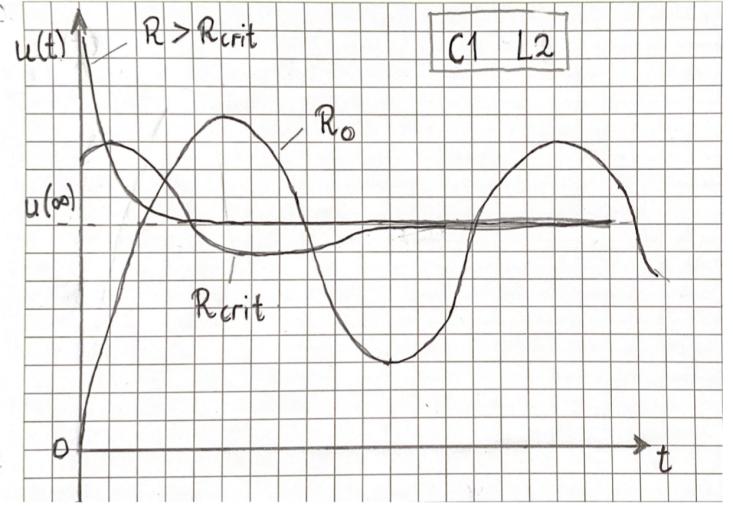
Observed currnet characteristic

C2 L2

$f_{IN} = 186Hz$
$T_{resp} = 0.46ms$
Measurement of oscillation period

Critical response $R_{crit} = 470\Omega$

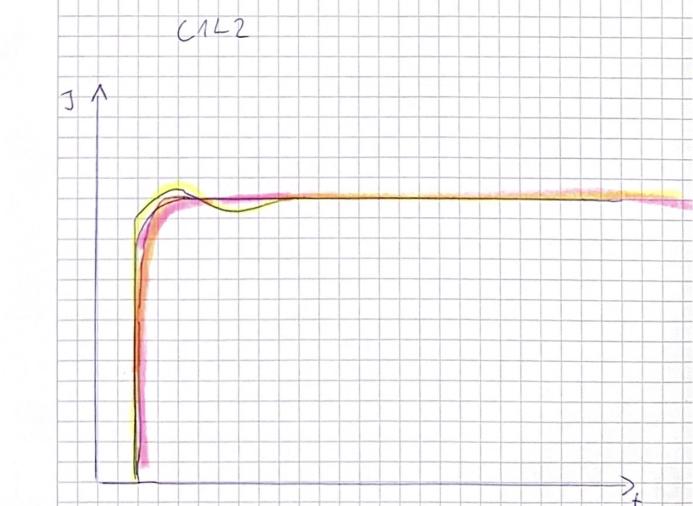
Observed voltage characteristic

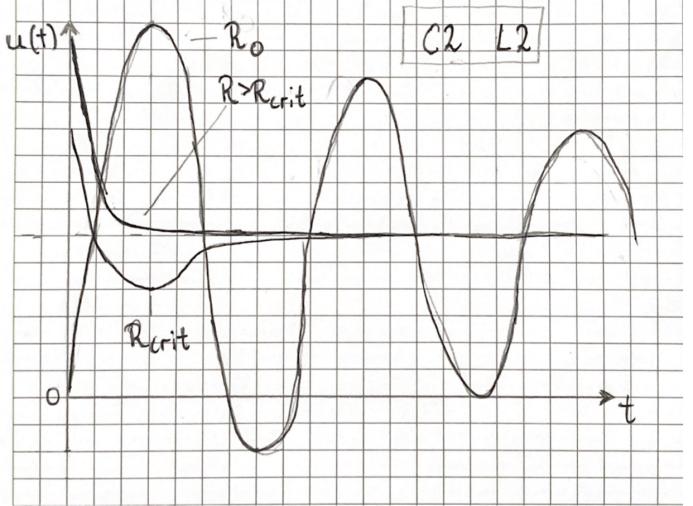
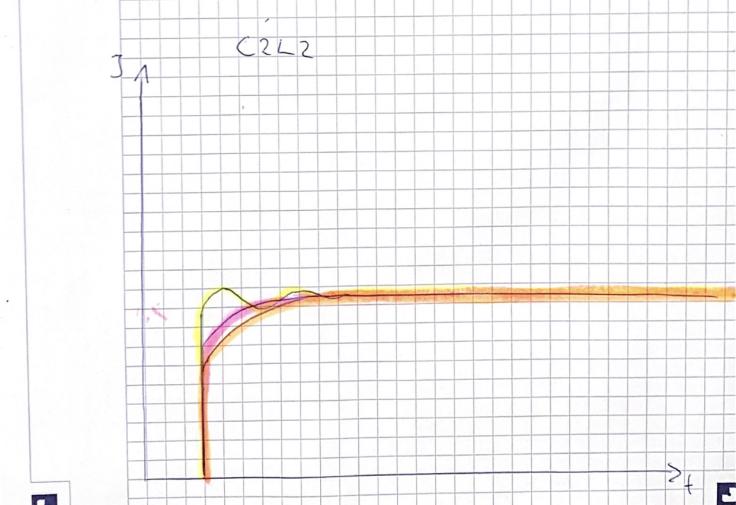
Observed currnet characteristic

C1C2 L2

$f_{IN} = 186Hz$
$T_{resp} = 1.16ms$

Critical response $R_{crit} = 130 \Omega$

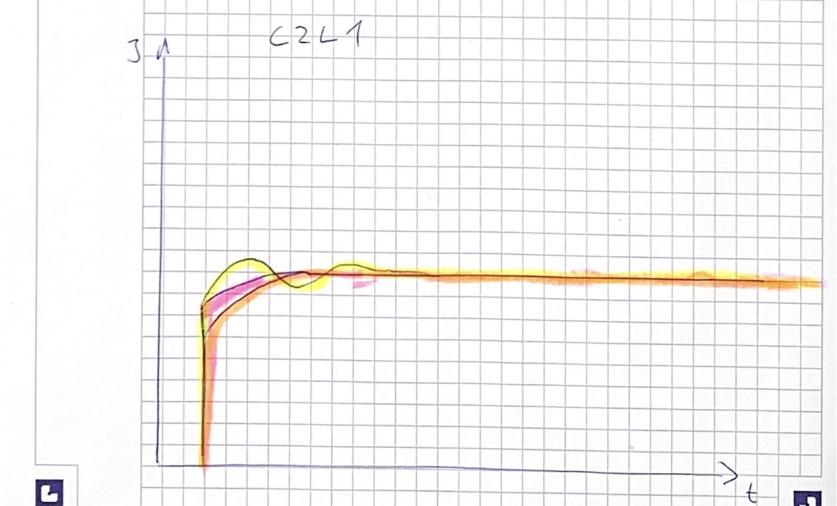
Observed voltage characteristic

Observed currnet characteristic

C2 L1

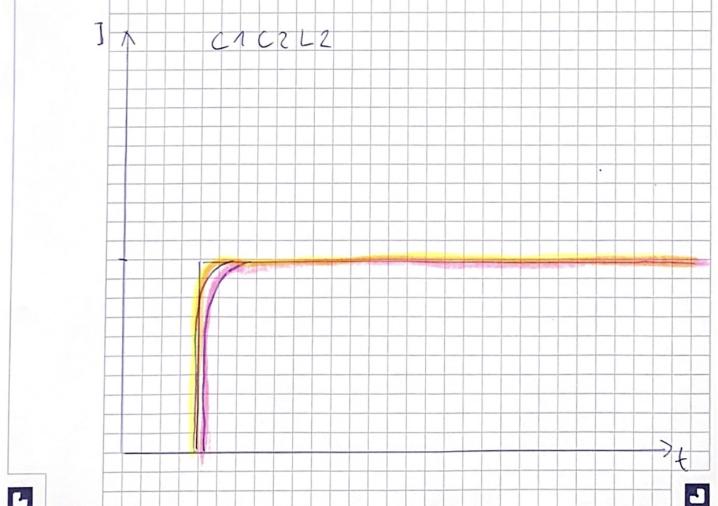
$f_{IN} = 186Hz$
$T_{resp} = 0.9ms$

Critical response $R_{crit} = 980 \Omega$

Observed voltage characteristic

Observed currnet characteristic

Data

$C1 = 749nF$
$C2 = 149nF$
$C1 \| C2 = 898nF$
$L1 = 130mH$
$L2 = 34mH$

$R_{L1} = 200\Omega$
$R_{L2} = 90\Omega$
$R_p = 12\Omega$
$R_d = 4k\Omega$

$U_A = 5.163V$

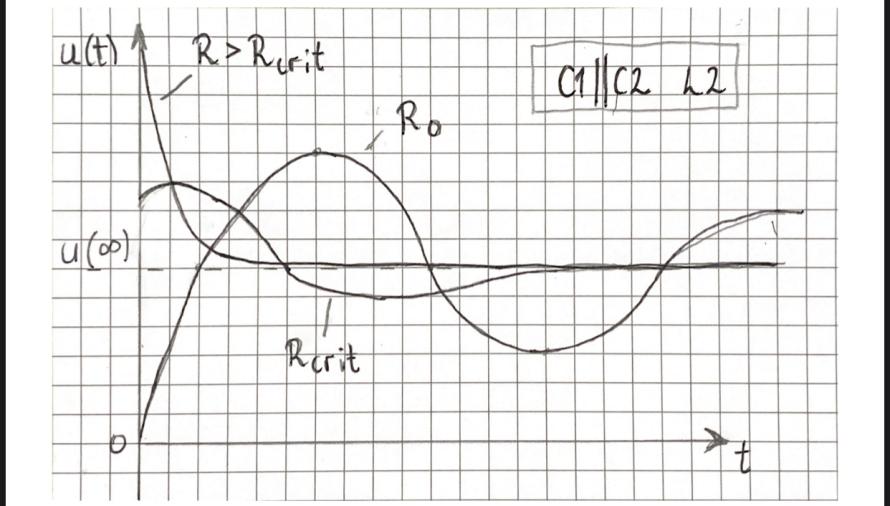
Configuration	C1 L2		C2 L2		C1C2 L2		C2 L1
x	Exp.	Calc.	Exp.	Calc.	Exp.	Calc.	Exp.	Calc.
Time period of osc. $R_0$	$1.04ms$	-	$0.46ms$	-	$1.16ms$	-	$0.9ms$	-
Freq. of osc. $R_0$	$961.5Hz$	$997.3Hz$	$2173Hz$	$2236Hz$	$862.1Hz$	$910.8Hz$	$1111Hz$	$1143Hz$
$\delta$	-	$-2.09$	-	$-0.4382$	-	$-2.647$	-	$-1.663$
$R_{crit}$	$150\Omega$	$339.337\Omega$	$470\Omega$	$897.346\Omega$	$130\Omega$	$391.826\Omega$	$980\Omega$	$192.966\Omega$
$i(0+)$ for $R_0$	$2mA$	$1.084mA$	$0.833mA$	$1.084mA$	$2.5mA$	$1.084mA$	$2.5mA$	$1.084mA$
$u(0+)$ for $R_0$	$0V$	$0V$	$0V$	$0V$	$0V$	$0V$	$0V$	$0V$
$i(\infty)$ for $R_0$	$2mA$	$1.063mA$	$1.66mA$	$1.063mA$	$2.5mA$	$1.063mA$	$2.5mA$	$1.039mA$
$u(\infty)$ for $R_0$	$200mV$	$95.7mV$	$200mV$	$95.7mV$	$200mV$	$95.7mV$	$400mV$	$207.8mV$
$i(0+)$ for $R_{crit}$	$1mA$	$1.06mA$	$2.083mA$	$1.031mA$	$2.5mA$	$1.062mA$	$1.66mA$	$0.9844mA$
$u(0+)$ for $R_{crit}$	$800mV$	$112.9mV$	$1000mV$	$289.8mV$	$700mV$	$103.3mV$	$1800mV$	$459.8mV$
$i(\infty)$ for $R_{crit}$	$1.833mA$	$1.063mA$	$1.833mA$	$1.063mA$	$1.833mA$	$1.063mA$	$2.083mA$	$1.039mA$
$u(\infty)$ for $R_{crit}$	$200mV$	$95.7mV$	$200mV$	$95.7mV$	$200mV$	$95.7mV$	$200mV$	$207.8mV$

Conclusions

If capacitance is growing, then the frequency is getting lower and so is $R_{crit}$.

If inductance is growing, then the frequency is dropping and so is $R_{crit}$.

Great difference between our observed and calculated values comes from low precision of setting the amplitude as well as invalid initial description of ‘critical damping’. From the laboratory instruction we gathered that it occurs when voltage passes the $u(\infty)$ line only once, however from calculations it appears that said line shouldn’t be crossed when searching for $R_{crit}$.