Report

Group: 2
Section: 6

Wojciech Bieniek
Patryk Piwowarczyk
Aleksandra Szpiech

Ex. 4

Tutor name: Damian Grzechca

Simulation responses

After setting initial variables such as frequency and amplitude we tested all three circuit configurations. Following are observations of coil powered by switching DC source without and with overvoltage protection

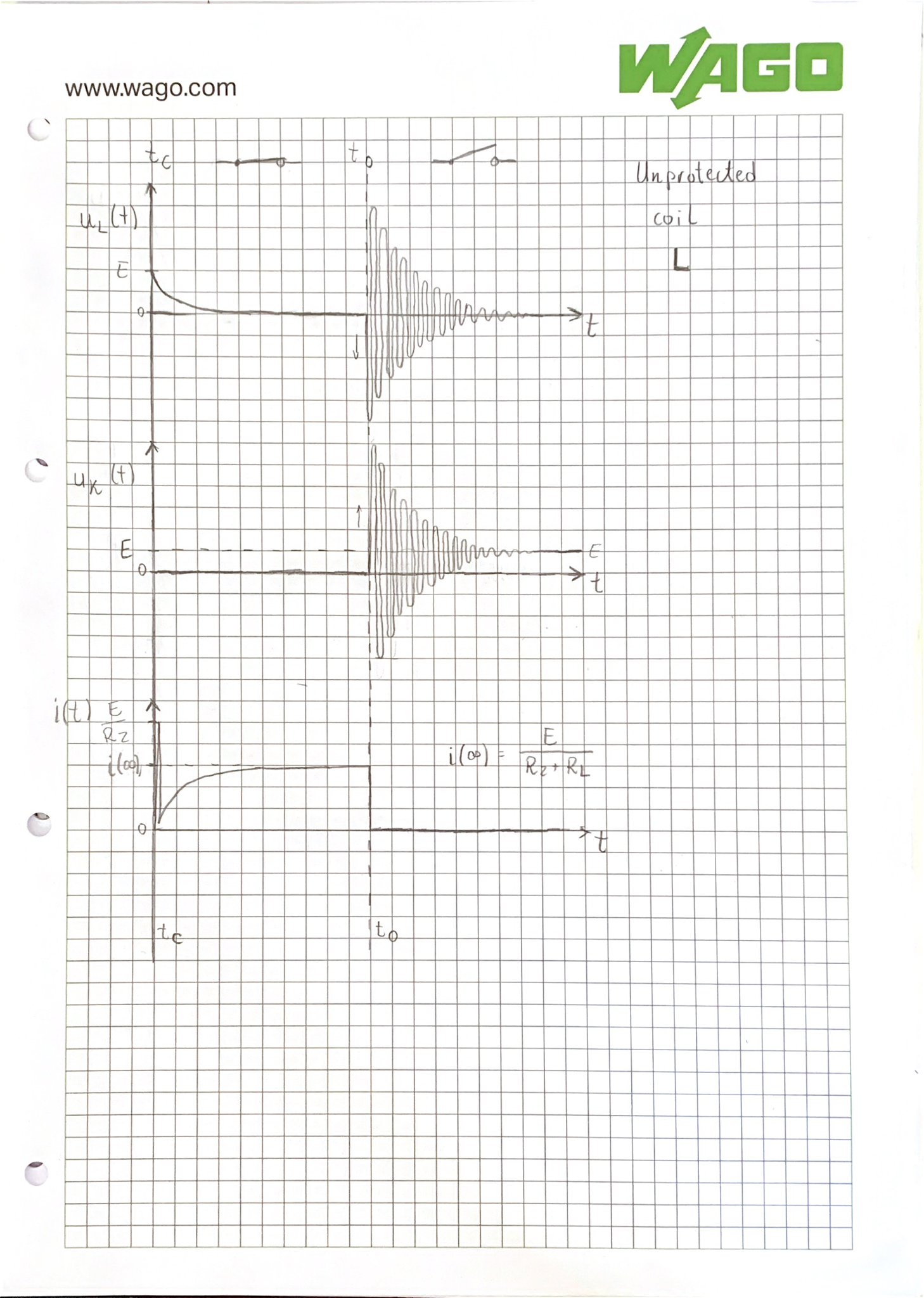
Unprotected coil

Observed responses for RL circuit with no overvoltage protection.

Characteristic of non-protected RL circuit

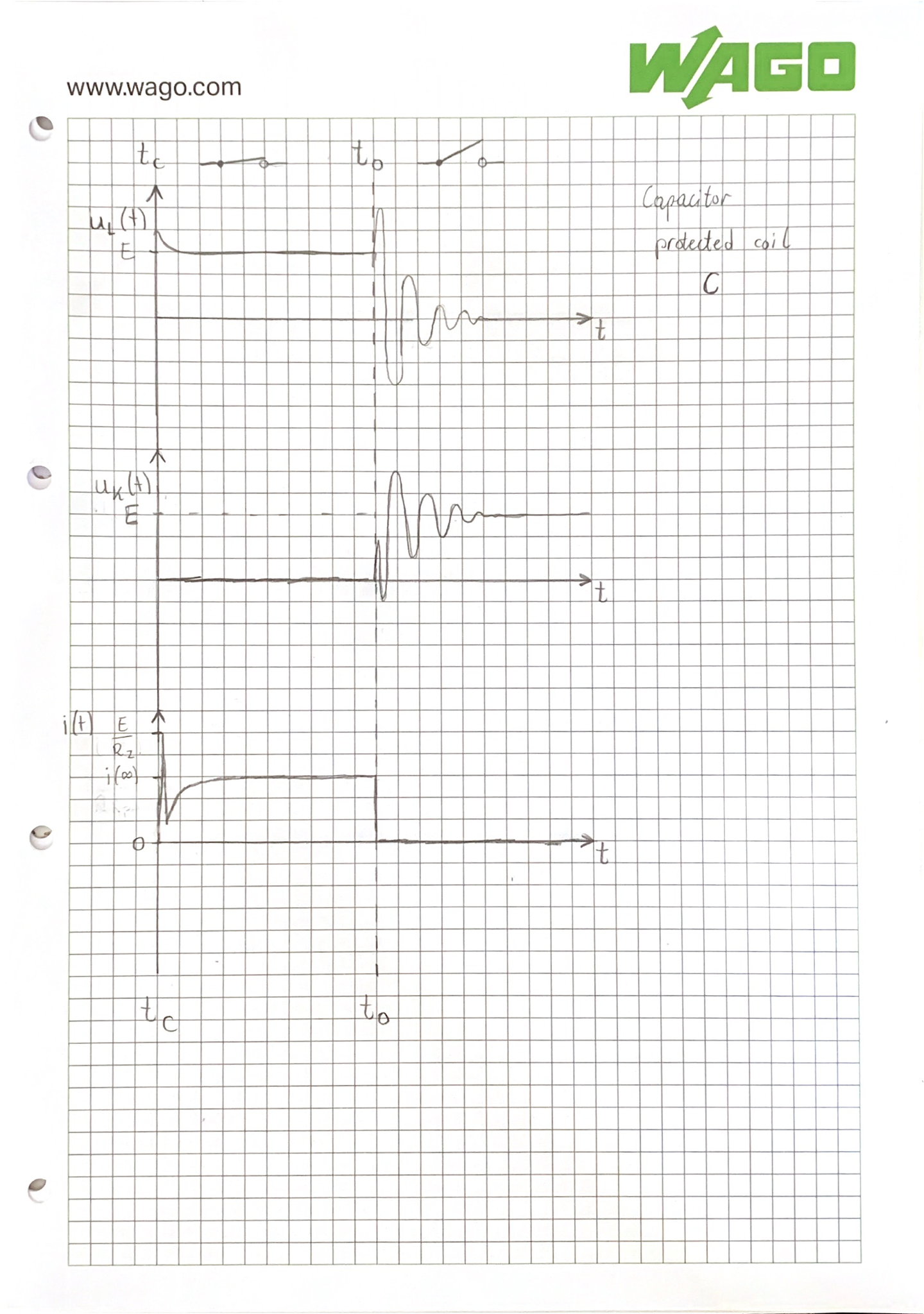
Capacitor protected

Observed responses for RL circuit with parallel capacitor.

Characteristic of capacitor protected RL circuit

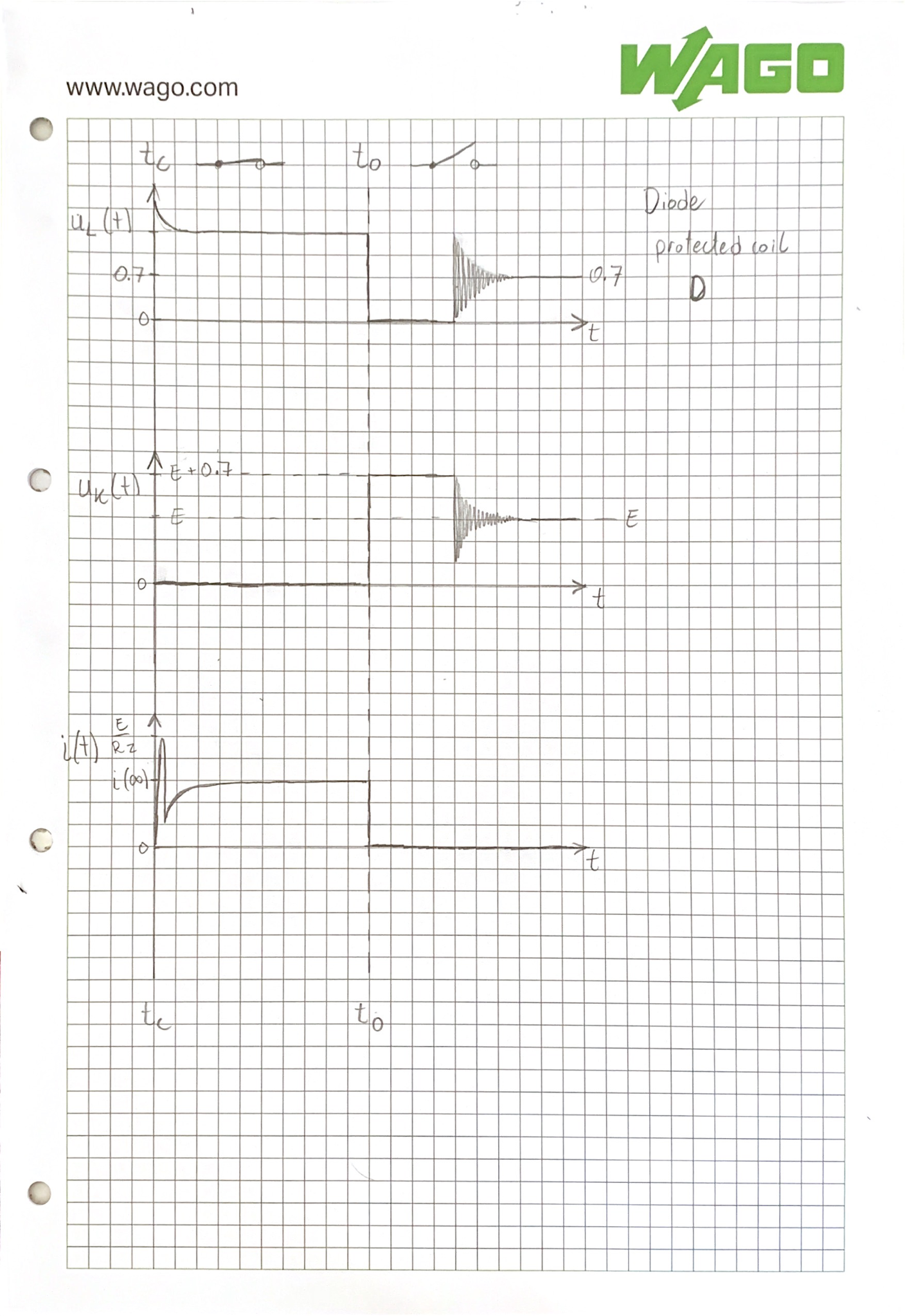
Diode protected

Observed responses for RL circuit with parallel diode.

Characteristic of diode protected RL circuit

Data

$R_P = 10 \Omega$
$R_z = R_P + R = 190\Omega$
$f_{IN} = 44.3 Hz$
$U_{gen} = 5.935 V$
Offset $= 2.983 V$

Circuit configuration	Unprotected	Capacitor	Diode
Oscilation period	$20 \mu s$	$2.1 ms$	—
Overvoltage value $[V]$	$150$	$2.4$	$2.2$

Observations description

In this RL circuit we observe the following behaviours, unexpected in an ideal circuit, yet apparent in all real coils.

Current spike

When the relay is closed, coil’s shunt capacitance acts as a short circuit, skipping coils internal resistance. Therefore the current spike reaches a value of ${E \over R_z} = {1.5V \over 190\Omega} \approx 8mA$.

Overvoltage ratio

For an unprotected coil the firtst oscilation period voltage on switch opening reaches 100 times the source value.
This value, as well as the oscillation frequency is decreased by a parallel capacitor to 2.4V, reaching 1.6 times the source value.
The most reliable high voltage protection is provided by a parallel diode, as the voltage drop over it cannot exceed 0.7V. Therefore the ratio is ${2.2\over1.5} = 1.46$ times the source voltage.

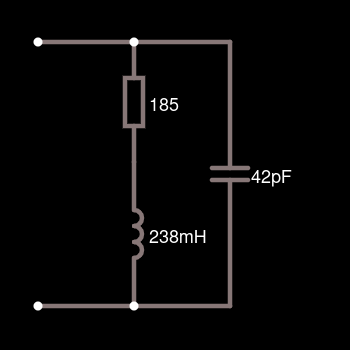
Coil properties

$\omega = {1 \over \sqrt{LC}} \implies LC = {1 \over (2\pi f)^2}$

$L = {1 \over (2\pi f)^2\times C} = {1 \over (2\pi\times {1\over0.0021})^2 \times 470\times 10^{-9}} = 237.6 [mH]$
$C_{shunt} = {1 \over (2\pi f)^2\times L} = {1 \over (2\pi{1\over0.000020})^2 \times 0.2376} = 42.64 [pF]$

$R_L = {u(t) \over i(t)} - R_z = {1.5V \over 4mA} - 190\Omega = 185[\Omega]$

Real coil model

Conclusions

Coil can be used to generate 100 times the source voltage, which can be used for creating high voltage impulses.
If we however choose to use different properties of the coil, to which this behaviour might be harmful, we can protect our circuits from voltage spikes by using capacitors or diodes. Both have their advantages.
Capacitors have oscillating transition to the steady state, and can produce negative voltage, however if the capacitance is picked correctly, it can be smoother. Where capacitor protection excells is keeping the steady state flat.
Diodes on the other hand have perfect transition from $0$ to $E+0.7$, however oscillations on them do appear later, when transitioning from $E+0.7$ to $E$. Those oscillations are of much higher frequency than on an unprotected coil. Such behaviour could in some situations affect other parts of the circuit.